Zagadki Krystalograficzne Rozwiązania
-
Rozwiązanie:
Żeby się o tym przekonać, to przypatrzmy się wpierw obu typom sieci przedstawionym w takich bazach wektorowych, w których opisane są one przez komórki elementarne typu P.
Oznaczmy wektory bazowe sieci typu F jako: a, b, c. Aby skonstruować komórkę prymitywną można jako końce wektorów bazowych wybrać węzły centrujące poszczególne ściany sąsiadujęce z początkiem układu współrzędnych. Jeżeli te nowe wektory oznaczymu jako: a', b', c', to wyrażą się one następujące przez wektory a, b, c:
a' = 1/2(b + c)
b' = 1/2(c + a)
c' = 1/2(a + b)
Podobnie dla sieci typu I oznaczmy wektory definiujace sieć prymitywną jako: a", b", c" i zdefiniujmy je tak, że łączą poczatek układu współrzędnych z odpowiednimi węzłami centującymi objętościowo tę sieć. Można te wektory wybrać następująco:
a" = 1/2(-a + b + c)
b" = 1/2( a - b + c)
c" = 1/2( a + b - c)
Sieć odwrotną najłatwiej jest skonstruować posługując się prymitywną komórką elementarną.
W takim przypadku sieć odwrotna do sieci typu F zgodnie z definicją będzie będzie oparta na wektorach:
a'* = 1/V' (b' x c')
b'* = 1/V' (c' x a')
c'* = 1/V' (a' x b')
gdzie x oznacza iloczyn wektorowy.Jeżeli wykonamy te iloczyny wektorowe podstawiając za a', b' i c' odpowiednie wyrażenia, to okaże się, że otrzymamy wektory, które są proporcjonalne do wektorów a", b" i c", czyli do wektorów definiujące sieć typu I.
Qed. -
Rozwiązanie:
Na etapie określania komórki elementarnej mamy pewną niejednoznaczność: jeżeli wybierzemy a, b, c, beta (na załączonym rysunku - czerwone wektory), to równie dobrze możemy wybrać a’=-a, b’=b, c’=-c, beta'=beta (a’, b’, c’ - zielone wektory). W obu przypadkach parametry komórki elementarnej w sensie warości skalarnych są takie same. Różnią się tylko orientacją (obrotem o 180 stopni wokół b).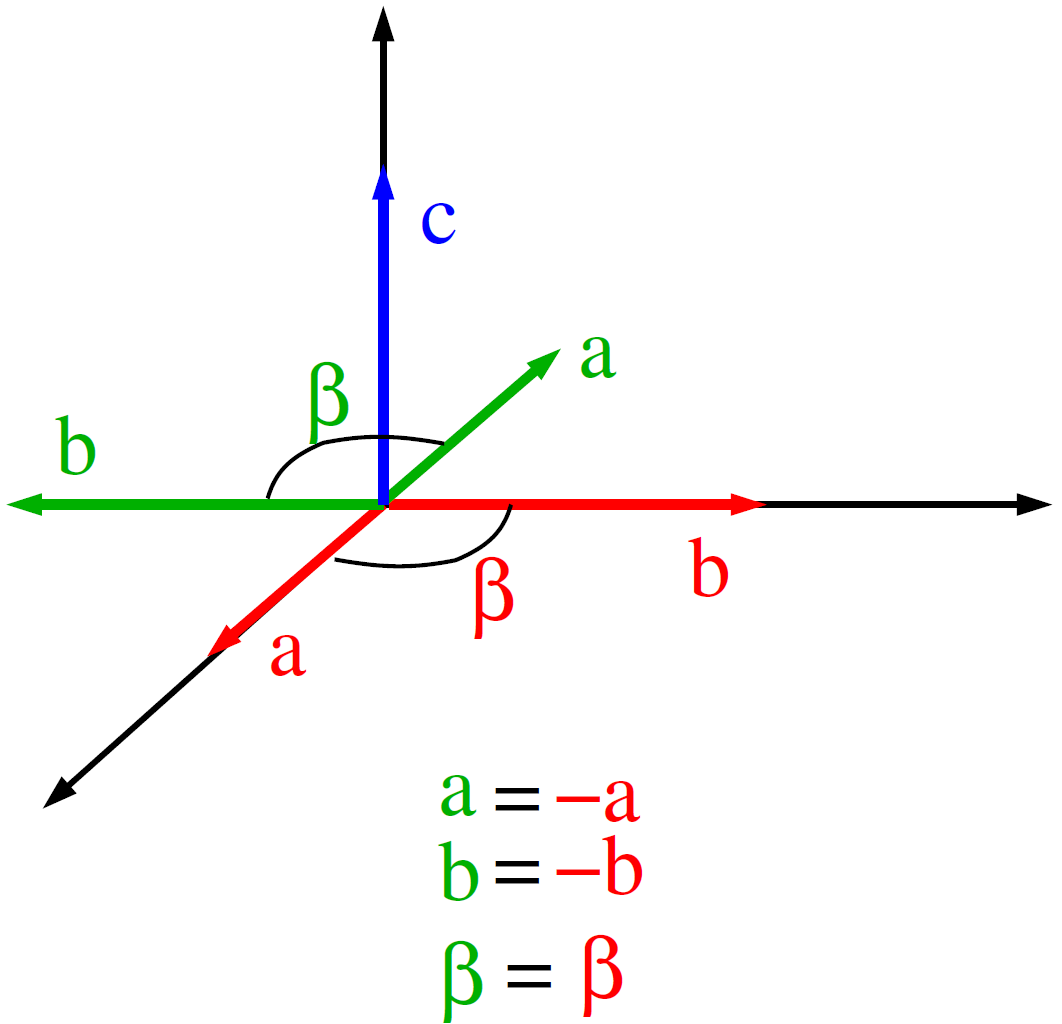
Te dwa wybory prowadzą do różnic w indeksowaniu refleksów. Ten sam refleks który w pierwszym przypadku ma indeks hkl, w drugim będzie miał -h k -l, a są to refleksy nierównoważne (jeżeli efekt rozpraszania anomalnego jest niezerowy). Tym sposobem wszystkie różnice Bijvoeta, F(hkl)-F(-h -k -l), zmieniają znak, a to prowadzi do odmiennych wartości parametru Flacka.
W efekcie, jeżeli każdy ze studentów postepował prawidłowo (parametr Flacka równy zero), to otrzymali struktury, które łączy obrót o 180 stopni wokół b. To oznacza, że parametr Flacka w przypadku grup niechiralnych informuje jedynie o orientacji struktury.
-
Rozwiązanie:
Nie ma żadnej sprzeczności w przeciwnych znakach kątów torsyjnych w badanej strukturze, bo oczywiście obaj doktoranci wyznaczyli tę samą strukturę tylko inaczej wybrali tzw. część niezależną komórki elementarnej. Jeden z nich wybrał (a raczej program rozwiązujący wybrał) cząsteczkę z kątem O1—C7—C8—C13 równym 59.7 stopnia, a drugi wybrał cząsteczkę będacą inwersyjnym obrazem tej pierwszej (grupa Pbca zawiera przecież środek symetrii). -
Rozwiązanie:
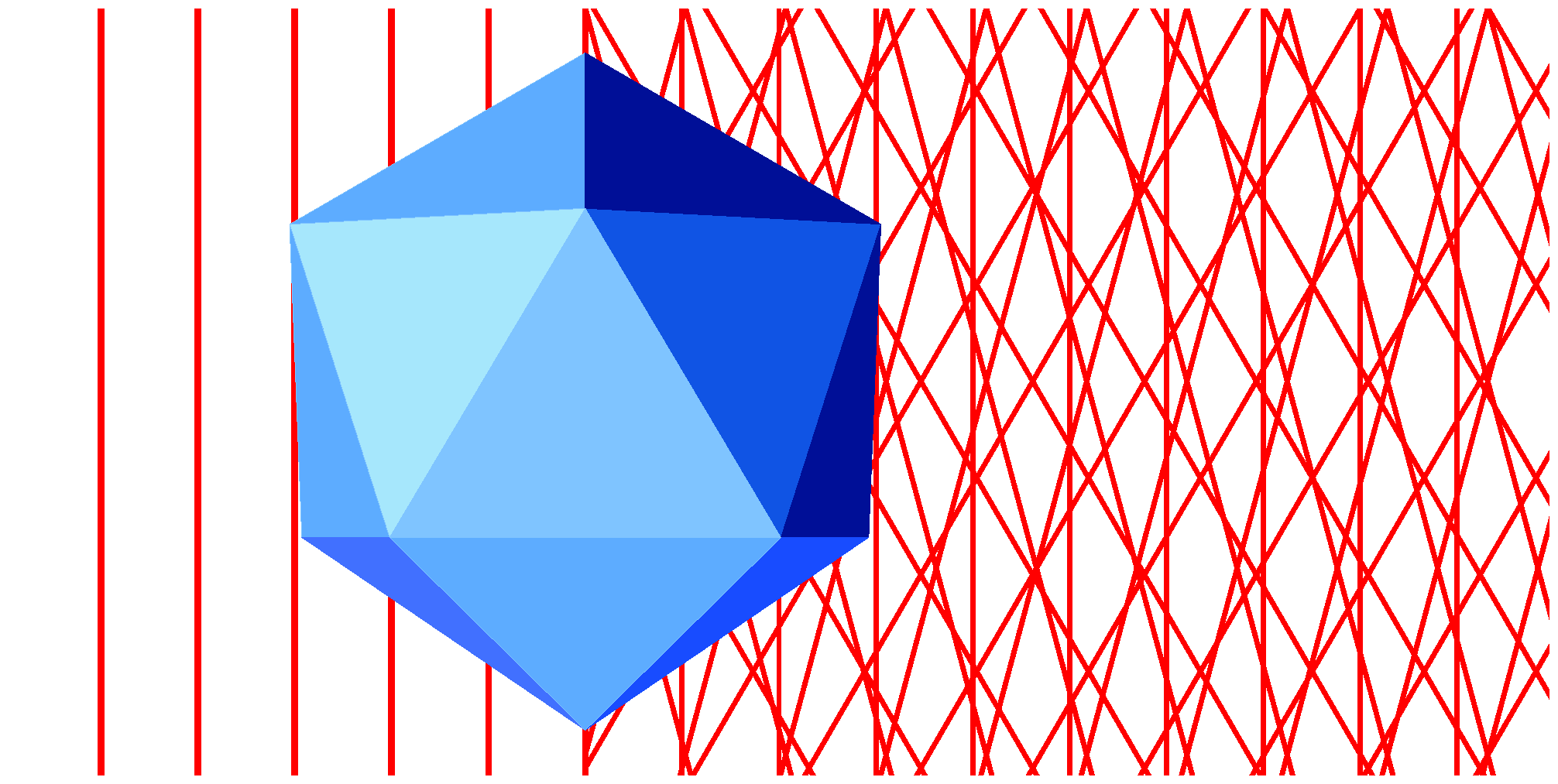
Jeżeli założymy, że poszerzenie refleksu wynikające z konstrukcji przyrządu jest zaniedbywalne, to odpowiedź na pytanie drugie jest prosta: rozmiary liniowe refleksów dyfrakcyjnych są proporcjonalne do długości fali użytego promieniowania. Średnica refleksu na detektorze dla promieniowania molibdenowego, D1, bedzie więc około dwa (0.71/1.54) razy mniejsza niż dla - miedziowego, D2. Wynika to wprost z konstrukcji Ewalda.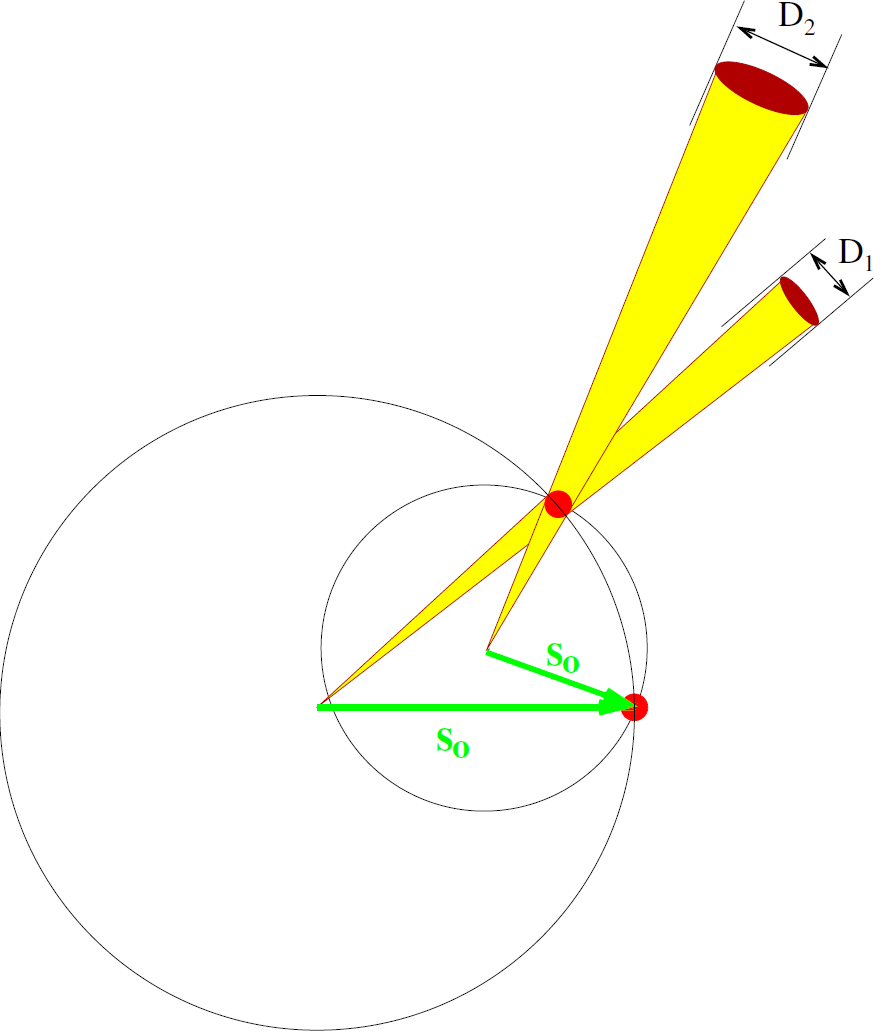
Na załączonym rysunku czerwone kółka odpowiadają węzłom w sieci odwrotnej, a żółte stożki odpowiadają wiązce promieniowania. Wysokości tych stożków opisujące odległość kryształu od detektora są równe.
Odpowiedź na pierwsze pytanie jest trochę bardziej złożona. Na pierwszy rzut oka stosunek intensywności rozproszonych I_Cu do I_Mo powinien być równy kwadratowi stosunku lambda_Cu do lambda_Mo, bo pola powierzchni refleksów na detektorze mają taki właśnie stosunek (D2/D1)^2. I jest to - w zasadzie - wniosek prawidłowy, ale z pewnymi zastrzeżeniami. Po pierwsze, sprawę komplikuje fakt, że ten sam refleks dla każdej długości fali biegnie pod innym kątem rozpraszania 2theta, w konsekwencji zarówno czynnik Lorentza jak i czynnik polaryzacyjny przyjmują inne wartości. Różnice te mają najmniejsze znaczenie dla refleksów niskokątowych. Po drugie, absorpcja promieniowania w detektorze, D_A, i czułość detektora, D_S, mogą zależeć od długości fali.
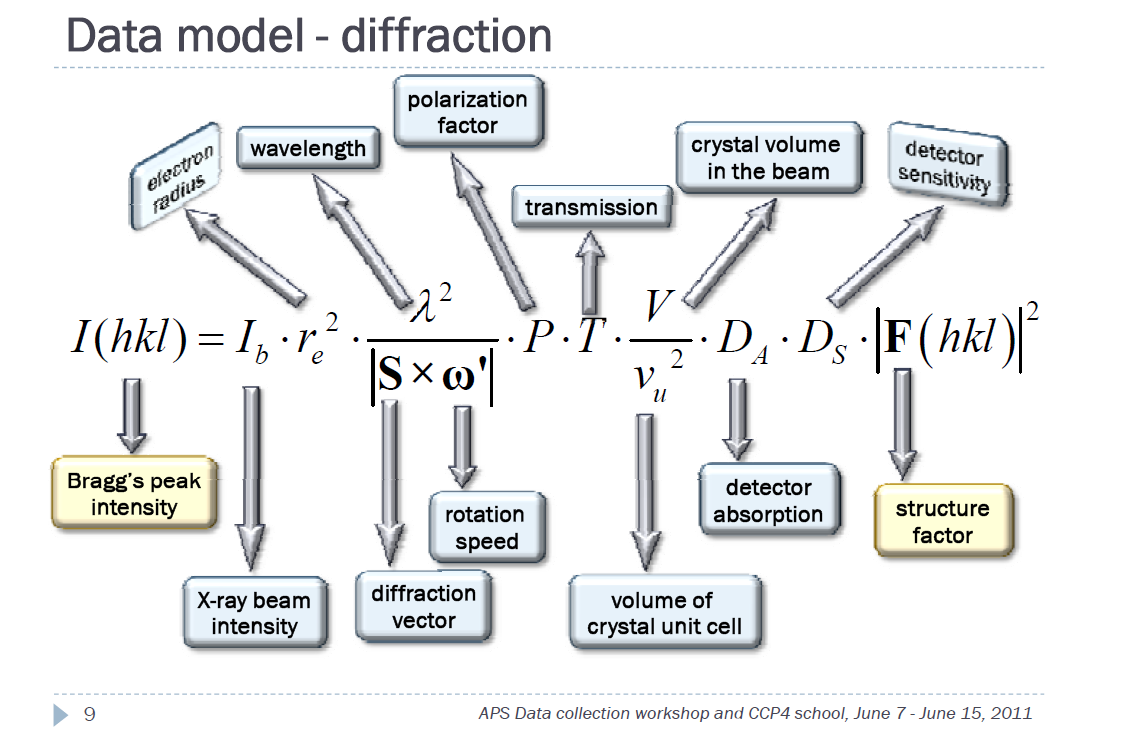
W niektórych podręcznikach (np. van Meerssche, str. 454) wzór na intesywność promieniowania rozproszonego podawany jest w postaci sugerującej zależność tej intesywności od trzeciej potęgi długości fali, ale w kontekscie postawionego pytania wniosek taki jest nieuprawniony.
-
Rozwiązanie:
Ponieważ elipsoida niezależnie od orientacji ma środek symetrii, więc jej położenie na środku symetrii nie wymaga spełnienia żadnych dodatkowych warunków. Inaczej jest z osią dwukrotną - jeżeli atom na niej leży orientacja elipsoidy musi być taka, aby jedna z jej osi głównych leżała na osi dwukrotnej.Formalnie tensor drugiego rzędu (a takim jest anisotropowy tensor drgań termicznych U) aby zachować niezmienniczość pod wpływem operacji symetrii musi spełniać warunek:
F*U*F(T) = U (1)
gdzie F oznacza macierz operacji symetrii a F(T) - macierz transponowaną.
Macierz F dla osi dwukrotnej leżącej wzdłuż kierunku [110] ma postać:
|0 1 0|
|1 0 0|
|0 0 -1|Zastosowanie równania (1) dla tego przekształcenia prowadzi do warunków:
U_11 = U_22
U_13 = -U_23 -
Rozwiązanie:
Fakt który od razu zwraca uwagę to kąt beta bardzo bliski wartości 90 stopni (beta=90.259), co dla układu jednoskośnego jest dość rzadką sytuacją. Powoduje to możliwość wzrostu dwu domen kryształu obróconych o 180 stopni wokół osi X lub Z, których refleksy dyfrakcyjne nakładają się niemal idealnie (bliźniak pseudomeroedryczny). Takie zbliźniaczenie zachowuje zarówno wygaszenia osiowe i płaszczyznowe, co oznacza, że grupa przestrzenna P2(1)/c jest wyznaczona prawidłowo. Wyjaśnia to też dziwną obserwację,że dla dużej grupy refleksów zmierzone Fo^2 są dużo większe od wartości obliczonych Fc^2. Wynika to z faktu, że nałożenie refleksu silnego ze słabym produkuje refleks silny, refleksu silnego z silnym - silny i tylko nałożenie dwu reflesów słabych produkuje refleks słaby. W ten sposób zmniejsza się populacja refleksów słabych.Podejrzenie, że za słabym udokładnianiem kryje się zbliźniaczenie okazało się słuszne. Zastosowanie instrukcji TWIN 1 0 0 0 -1 0 0 0 -1 prowadzi do udokładnienia struktury z czynnikiem rozbieżności R1 = 0,035. Podczas udokładniania okazało się, że udział obu domen wynosi 0,75:0,25 w przybliżeniu.
-
a(1)*, a(2)*, a(3)* oznaczają wektory bazy sieci odwrotnej: a*, b* i c* odpowiednio.
Dla pierwszej domeny z definicji macierzy orientacji, U, mamy:
[ a(1)* a(2)* a(3)* ] = [ e(1) e(2) e(3) ] * U (równanie 1)
Dla drugiej domeny (oznaczonej primem) macierz orientacji oznaczmy jako U':
[ a(1)*' a(2)*' a(3)*' ] = [ e(1) e(2) e(3) ] * U' (równanie 2)
Pomnóżmy teraz pierwsze równanie prawostronnie przez U(-1),czyli macierz odwrotną do U. W rezultacie otrzymamy:
[ a(1)* a(2)* a(3)* ] * U(-1) = [ e(1) e(2) e(3) ] (równanie 3)
wstawmy wyznaczone w ten sposób [ e(1) e(2) e(3) ] do równania drugiego. Otrzymamy wtedy:
[ a(1)*' a(2)*' a(3)*' ] = [ a(1)* a(2)* a(3)* ] * U(-1) * U'
W ten sposób otrzymaliśmy transformację łączącą domeny bliźniaka. Opisuje go iloczyn macierzy U(-1) * U'. Iloczyn ten po wykonaniu obliczeń przyjmuje postać:
|-1,002 0,004 0,004|
|-0,014 -1,000 0,002|
|-0,853 -0,578 1,002|Stosując metodę opisaną w rozwiązaniu zagadki nr 4 można ustalić, że macierz ta opisuje obrót o blisko 180 stopni wokół osi a(3)* czyli c*.
Rozwiązanie cz.2:
Żeby znaleźć stałe sieciowe kryształu wystarczy określić postać macierzy metrycznej G. Macierz G to z definicji macierz składająca się z iloczynów skalarnych wektorów bazowych sieci a(1), a(2) i a(3), czyli a, b i c:
|a(1).a(1) a(1).a(2) a(1).a(3)|
|a(2).a(1) a(2).a(2) a(2).a(3)|
|a(3).a(1) a(3).a(2) a(3).a(3)|Wyrazy diagonalne tej macierzy pozwalają wyznaczyć długości stałych sieciowych, a wyrazy pozadiagonalne - kąty między nimi.
Macierz tę znajdziemy nieco okrężną drogą. Najpierw skonstruujmy macierz metryczną, G*, dla sieci odwrotnej, a potem policzymy macierz G jako macierz odrotną do G*: G = G*(-1). G* to z definicji macierz, której wyrazy są iloczynami skalarnymi wektorów bazy sieciodwrotnej a(1)*, a(2)* i a(3)*.
|a(1)*.a(1)* a(1)*.a(2)* a(1)*.a(3)*|
|a(2)*.a(1)* a(2)*.a(2)* a(2)*.a(3)*|
|a(3)*.a(1)* a(3)*.a(2)* a(3)*.a(3)*|Macierz metryczna G* można przedstawić jako iloczyn dwu macierzy: jednokolumnowej i jednowierszowej:
|a(1)*|
|a(2)*| | a(1)* a(2)* a(3)*| = G* (równanie 4)
|a(3)*|przy czym wektor
|a(1)*|
|a(2)*|
|a(3)*|jest transpozycją wektora | a(1)* a(2)* a(3)*|.
Stosując transpozycję do równania definiującego macierz orientacji, czyli[ a(1)* a(2)* a(3)* ] = [ e(1) e(2) e(3) ] * U
otrzymamy:
|a(1)*| |e(1)|
|a(2)*| = U(T) |e(2)|
|a(3)*| |e(3)|gdzie U(T) oznacza macierz transponowaną do U. Wstawiając tę zależności do równania (4) na G* i korzystając z faktu, że
|e(1)|
|e(2)| | e(1) e(2) e(3)| = 1 (macierz jednostkowa)
|e(3)|otrzymamy:
G* = U(T) * U
Tak więc macierz G* jest iloczynem transponowanej macierzy orientacji U(T) z samą macierzą orientacji U. I ostatecznie G = G*(-1).
Po wykonaniu obliczeń otrzymujemy:
|30,2515029325 1,1669100579 13,4398288704|
|1,1669100579 70,647868067 21,1250174688| = G
|13,4398288704 21,1250174688 155,3675840111|a w konsekwencji:
a = 5,50 A
b = 8,41 A
c = 12,46 A
alfa = 78,4 deg
beta = 78,7 deg
gamma = 88,6 deg
-
Wyjaśnienie tej sytuacji ilustruje najlepiej konstrukcja Ewalda dla kryształu dwuwymiarowego. Warunki dyfrakcji Lauego dla takiego kryształu przyjmują postać:
∆s · a = h
∆s · b = kBrak trzeciego warunku (∆s · c = l) sprawia, że konstrukcja Ewalda jest nieco inna niż w przypadku kryształu trójwymiarowego: aby wystąpiła dyfrakcja nie jest konieczne, aby węzeł sieci odwrotnej leżał na sferze Ewalda - wystarczy, że linia prostopadła do kryształu, przechodząca przez węzeł sieci odwrotnej przecina sferę Ewalda (Rys. 1). Wyjaśnienie tej modyfikacji podane jest na końcu rozwiązania.
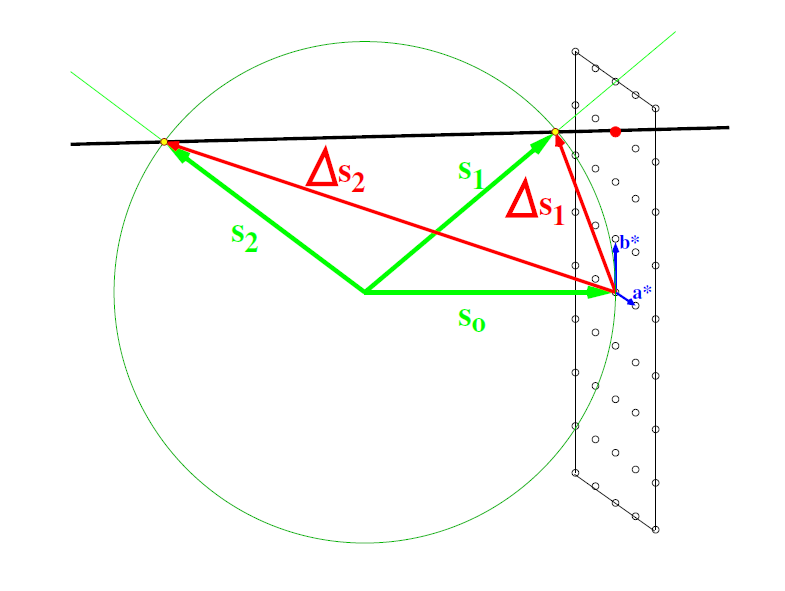
Rysunek 1: Dyfrakcja ma miejsce w kierunkach s1 i s2 wyznaczonych przez przeciecie sfery Ewalda przez linie prostopadła do kryształu i przechodzaca przez wezeł sieci odwrotnej (czerwony punkt).Przy okazji mozna w tym miejscu poczynic dwie ciekawe obserwacje:
1. jednemu wezłowi sieci odpowiadaja dwa promienie dyfrakcyjne, gdyż linia prostopadła do kryształu przecina sfere Ewalda w dwóch punktach (Rys. 1),
2. dla kryształów dwuwymiarowych nie istnieje odpowiednik prawa Bragga, gdyż refleks o określonym wskaźniku hk można obserwować pod różnymi kątami 2theta w zależności od nachylenia kryształu w stosunku do wiązki promienia padającego.
Wyjasnienie zagadki jest czysto geometryczne, gdyż przy zmianie kata nachylenia kryształu mozna zauwazyc, ze punkt przeciecia lini prostopadłej dla refleksu niskokatowego („przechodzacego do przodu”) tylko nieznacznie zmienia swoje połozenie, natomiast punkt przeciecia refleksu wysokokatowego („odbitego do tyłu”) zmienia połozenie bardzo znaczaco (Rys. 2).
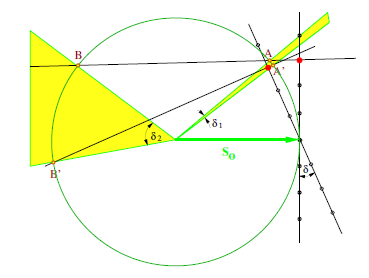
Rysunek 2: Linia prostopadła do powierzchni kryształu przechodzaca przez wezeł
sieci odwrotnej (czerwony punkt) przecina sfere Ewalda w dwu punktach:
A i B. Kryształ poczatkowo ustawiony prostopadle do padajacej wiazki promieniowania, so, nachylamy o kat delta. Teraz linia prostopadła do kryształu przecina sfere Ewalda
w punktach A' i B'. W efekcie obserwujemy niewielka zmiane, delta1, w kacie rozpraszania dla refleksu niskokatowego i duza zmiane, delta2, dla refleksu wysokokatowego.Wyjasnienie konstrukcji Ewalda w 2D.
Wektor ∆s mozna rozłozyc na dwie składowe: równoległa do powierzchni kryształu, ∆s||, i prostopadła do tej powierzchni, ∆s_I_ (Rys. 3). Warunki Lauego mozna wiec przedstawic w nastepujacej formie:(∆s||+ ∆s_I_) · a = h
(∆s|| + ∆s_I_) · b = kPoniewaz wektor ∆s_I_ z definicji jest prostopadły do wektorów a i b, to odpowiednie iloczyny skalarne sa równe zero: ∆s_I_· a = ∆s_I_· b = 0. W konsekwencji składowa prostopadła nie ma wpływu na spełnienie warunków dyfrakcji, a wiec moze byc dowolna. Do spełnienia warunków dyfrakcji wystarczy, aby wektor ∆s|| był równy wektorowi sieci odwrotnej H = ha* + kb*, gdyż H·a = h i H·b = k. Warunki dyfrakcji mozna wiec ostatecznie zapisac w postaci jednego równania wektorowego:
∆s|| = H
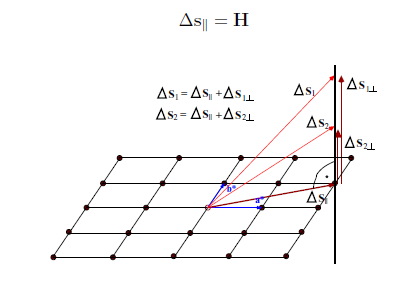
Rysunek 3: Dowolny wektor ∆s którego koniec lezy na lini prostopadłej do kryształu przechodzacej przez wezeł sieci spełnia warunek Lauego ∆s|| = H.
-
Jest to obrót inwersyjny o 90 stopni wokół osi leżącej wzdłuż kierunku [-1 -1 2].
Rozwiązanie:
Aby rozwiązać zagadkę należy obliczyć dwie charakterystyki macierzy:
a) wyznacznik i
b) ślad
oraz
c) rozwiązać odpowiednie równanie własne.Do dzieła!
a) Zaczynamy od sprawdzenia wyznacznika, gdyż wszystkie przekształcenia symetrii można podzielić na dwie klasy: te z wyznacznikim równym 1 (przekształcenia pierwszego rodzaju, czyli przekształcenia nie zmieniające chiralności - są to zwykłe obroty) i te z wyznacznikiem równym -1 (przekształenia drugiego rodzaju, czyli zmieniajace chiralność - obroty inwersyjne).Oznaczmy rozpatrywaną macierz przez "A". Wyznacznik tej macierzy, det(A) = -1, co oznacza, że mamy do czynienia z przekształceniem drugiego rodzaju.
b) Ślad macierzy, Tr(A), dla przekształceń pierwszego rodzaju jest zawsze równy 2cos(phi) + 1, natomiast dla przekształceń drugiego rodzaju jest równy -2cos(phi) - 1, gdzie phi oznacza kąt obrotu. W naszym przypadku mamy więc:
Tr(A) = -2cos(phi) - 1
Tr(A) czyli suma elementów macierzy na głównej diagonalnej jest równa 0 + 0 + (- 1) = -1
Otrzymujemy więc równanie:-1 = -2cos(phi) - 1
którego rozwiązaniem jest phi=90. Mamy wiec do czynienia z obrotem inwersyjnym o 90 stopni.
c) Pozostaje do ustalenia kierunek wzdłuz którego leży oś obrotu. W tym celu wystarczy rozwiązać następujące równanie własne:Ar = -r,
gdzie r oznacza wektor o współrzędnych [xyz]. (W przypadku zwykłego obrotu byłoby to równanie: Ar=r.) Rozwiązanie tego równania wskaże nam poszukiwany kierunek, gdyż tylko wektory r leżące
na osi inwersyjnej przekształcają się pod wpływem obrotu w swoje przeciwieństwo, -r. Równanie to w zapisie macierzowym przyjmuje postać:| 0 1 1| |x| |-x|
| -1 0 0| |y| = |-y|
| 0 0 -1| |z| |-z|co prowadzi do następującego układu równań:
y+z = -x
-x = -y
-z = -zRozwiązaniem tego ukladu jest każdy wektor równoległy do wektora [-1 -1 2].
Komentarz:Postać macierzy przekształcenia symetrii zależy od układu współrzędnych, w którym ją wyrażamy. Macierz o której mowa w zagadce została wyrażona w niestandardowym układzie, w którym wybrano prymitywną komórkę elementaną zamiast komórki centrowanej objętościowo.
- Złożenie dwu odbić zwierciadlanych względem płaszczyzn prostopadłych prowadzi zawsze do powstania osi dwukrotnej równoległej do krawędzi przecięcia tych płaszczyzn. Czy będzie to oś zwykła, czy śrubowa decydują translacje ślizgowe rozpatrywanych płaszczyzn.
W grupie Pbnb oś dwukrotna równoległa do osi OX układu współrzędnych powstaje ze złożenia odbić względem płaszczyzn n_y i b_z. Mamy tu translacje: 1/2a + 1/2c dla płaszczyzny n_y i 1/2b dla płaszczyzny b_z. Występowanie translacji 1/2a powoduje, że powstaje oś śrubowa 2_x(1).
Oś dwukrotna równoległa do osi Y układu współrzędnych powstaje ze złożenia odbić względem płaszczyzn b_x i b_z. Mamy więc dwie translacje o 1/2b, co w sumie daje translację o stałą sieciową b i prowadzi do osi zwyczajnej 2_y.W przypadku osi 2_z(1) sytuacja jest analogiczna do przypadku osi 2_x(1). Prawidłowa jest więc odpowiedź c).
-
Rozwiązanie.
Przyjrzyjmy się sytuacji opisanej w zagadce na przykładzie czterokrotnej osi inwersyjno-śrubowej położonej wzdłuż osi Z. Poczatek ukladu współrzędnych wybieramy na środku inwersji. Pozycje równoważne generowane przez taki element symetrii są następujące:(I): (x,y,z); (y,-x,-z+1/4); (-x,-y,z); (-y,x,-z+1/4)
Natomiast zwykła oś czterokrotna inwersyjna generuje następujące pozycje równoważne:(II): (x,y,z); (y,-x,-z); (-x,-y,z); (-y,x,-z)
Na pozór zestawy pozycji (I) i (II) wydają się różne. Jednakże, gdy w przypadku zwykłej osi inwersyjnej przesuniemy początek układu współrzędnych w ten sposób, żeby środek symetrii zmienił swoje położenie z punktu (0,0,0) na położenie (0,0,1/8), to otrzymamy dokładnie zestaw pozycji (I).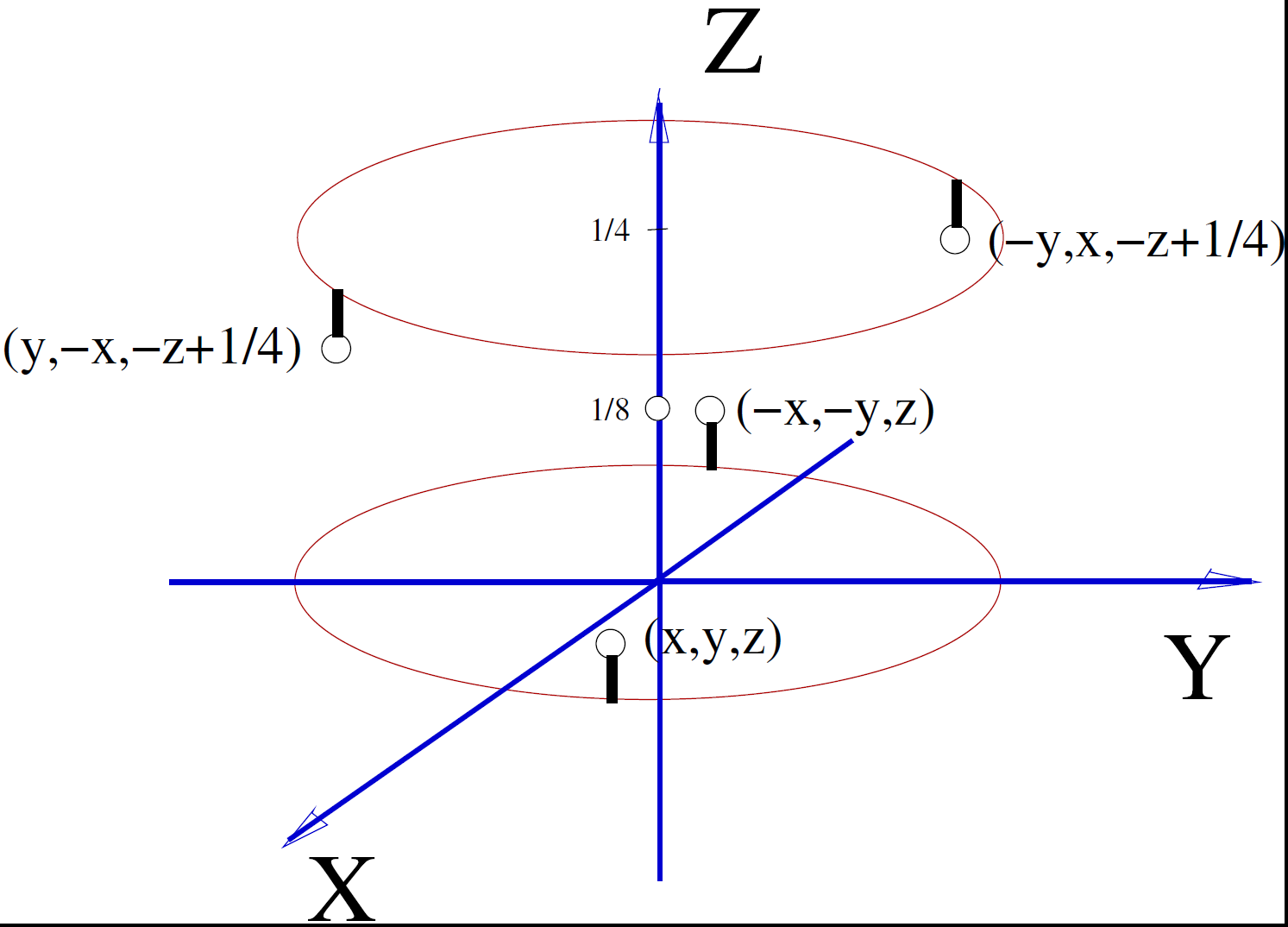
W konsekwencji oś inwersyjno-śrubowa jest zywkłą osią inwersyjną i nie ma potrzeby wprowadzania nowego elementu symetrii.
- Odpowiedź:
ściana ABC - (1 1 1)
ściana ABD - (1 1 -3)
ściana BCD - (-3 1 1)
ściana ADC - (1 -3 1)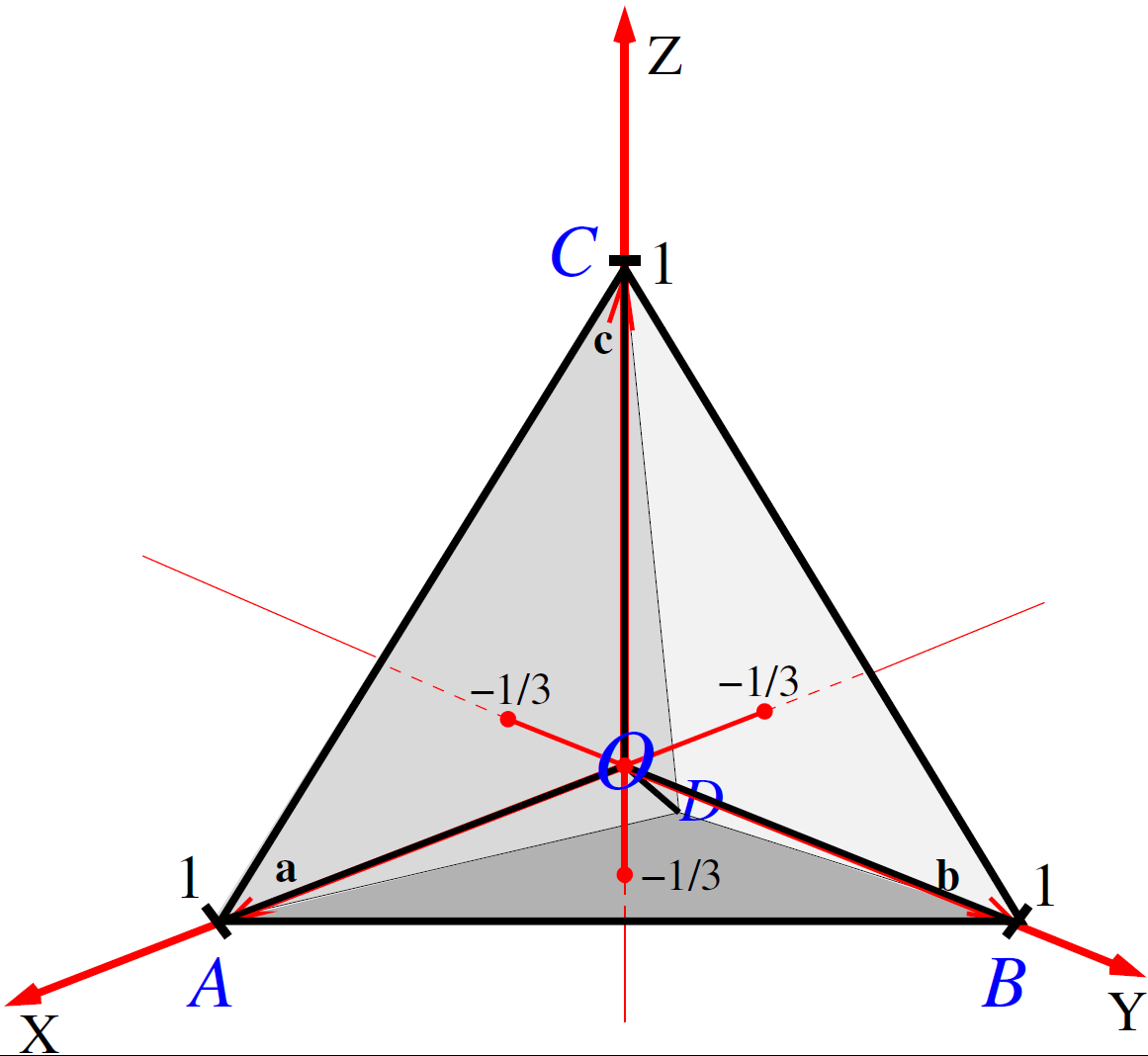
Rozwiązanie 1.
Kluczem do rozwiązania jest fakt, że wysokości w czworościanie foremnym (które - jak widać na rysunku - leżą na osiach X, Y i Z), przecinają się w punkcie O, który dzieli te wysokości na odcinki o stosunku długości 3:1. Z tego wynika, że poszczególne ściany przecinają odpowiednie osie w punktach o współrzędnych 1 lub -1/3 (rysunek). Z kolei fakt podziału w stosunku 3:1 łatwo stwierdzić zauważając, że objetość wyjściowego czworościanu można przedstawić jako sumę objętości czterech jednakowych ostrosłupów, których podstawami są ściany wyjściowego czworościanu, a ich wierzchołki leżą w punkcie przecięcia wysokości (punkt O) wyjściowego czworościanu.
Rozwiązanie 2.
Ponieważ ustalenie wskaźników ściany ABC (czyli (1 1 1)) jest trywialne, można zastosować również inne podejście - bardziej krystalograficzne. Polega ono na znalezieniu macierzy obrotu (co nie jest trudne) wokół trójkrotnych osi symetrii czworościanu i zastosowaniu ich do wskaźników pierwszej sciany (1 1 1).